How many interview rounds is too many?

It’s Hallowe’en; that time of year when LinkedIn is full of photos of the recruiters who ghosted you dressed up as ghosts. But ghosting isn’t the only bad thing about the modern-day job market. Another plague on job seekers is the endless rounds of interviews which companies put people through. A common scenario is that you do several interviews, only to be asked to do one more, and then one more, and then… One job seeker was even interviewed 29 times for a single position. Needless to say, she didn’t get it.

I’ve recently been studying the Solow Model of economic growth and I’m impressed by how much interesting information can be dervied from a simple model, even before any real data has been put into it. Can we do the same for job interviews? Is there a reason why companies demand that candidates attend so many interviews? If you’re in the middle of an interview process and the company requests one more interview, what should you do? Read on to find out!

The Model

Suppose a company is interviewing a single candidate. The candidate may be bad or good from the point of view of the company. The cost of hiring a bad candidate is $C$ and the cost of hiring a good candidate is $0$. The purpose of the interview process is to detect whether the candidate is bad. Let $p_i$ be the probability that interview $i$ detects a bad candidate. For simplicity, we’ll assume that all the interviews are independent and that the $p_i$ are all equal to a constant value $p$. The idea is that, after $k$ interviews, the probability that the candidate is bad is $(1-p)^k$.

Suppose that it costs the company $c$ to do an interview. Then the expected cost of hiring a candidate after $k$ interviews is

where the first term is the cost of hiring an undetected bad candidate and the second term is the cost of the interviews.

The optimal number of interviews can be obtained by setting the derivative to zero, which yields

as the ideal number of interviews.

Marginal Considerations

Perhaps it’s better to think like an economist and consider the marginal cost of the $k^{th}$ interview. The cost of interview $k+1$ is $C(1-p)^{k+1} + c(k+1)$ and the cost of interview $k$ is $C(1-p)^k + ck$. Subtracting one from the other yields the marginal cost $c - Cp(1-p)^k.$ The company will stop interviewing when this reaches zero, so we get $Cp(1-p)^k = c$ which gives

as the ideal number of interviews.

This function is increasing in $C/c$, which makes sense because you would expect to need more interviews if making the wrong hire was more expensive (for example, if hiring for a senior position or if hiring in a country with strong labour laws.) It is decreasing in $p$, which means that fewer interviews are required if the company is better at detecting bad candidates. But does it give sensible output?

Sanity Check

Let’s experiment with some numbers to see whether this makes sense. A 2016 Google study found that $4$ interviews was always enough to make a hiring decision. To find a value of $C$, suppose that the employee has a three-month probation period of $8$–hour days, and so the company will risk losing about $12 \times 5 \times 8 = 480$ hours of work if they hire the wrong person. Let’s say $C=500$ and $c=1$ (assuming an interview is $1$ hour of work).

Then we can find $p$ by solving $p(1-p)^4 = 1/500$, which suggests that, for Google, the probability of detecting a bad candidate in an interview is about $p= 0.77$, which seems reasonable.

What if Google wants to hire a new CEO? The annual salary of Google’s CEO including all benefits is about $200 \times 10^6$ dollars. Suppose Google stands to lose this much if they hire the wrong person, and suppose that an interview costs one hour of time for an employee who is paid $10^5$ dollars per year, which would be about $10^5/(52 \times 5 \times 8) \approx 50$. Then the optimal number of interviews is

Is this reasonable? I don’t know, but it’s nice that it didn’t come out to be a crazy number like, say, 29.

The Candidate’s Point of View

All this is nice, but does it really tell you what to do if you are a candidate? For example, suppose you have already done $6$ interviews. Now the company is asking you for a seventh. What are your chances of getting the job if you go along with their request? Is it really worth continuing to let them string you along?

Surprisingly, it’s possible to use the same model to get a rough answer to a question like this.

Credence

To start with, you need a probability distribution which expresses your belief about $p$. Suppose its density is $f(p)$. Perhaps you think $p$ could be anything, so $f(p)=1$. Perhaps you are interviewing at a company where you think $p=0.77$ and you use, say, a beta distribution with a mean close to $0.77$. Whatever $f$ you choose, this is your credence before the interviews start.

Now suppose you have already done $k$ interviews and not been hired. What can you conclude? You want to know the answers to questions like

• What is the probability that I get hired after one more interview?
• How many more interviews will I need to do?

Let’s assume you are a “good” candidate from the point of view of the company, so you will eventually get hired, it’s just a question of how many more rounds of interviews it takes. You’ve already done $k$ of them. Since you weren’t hired yet, the marginal cost of the last interview must be negative, so

which establishes an upper bound for $p$. If $p_0$ is such that $c = Cp_0(1-p_0)^k$ then $p \le p_0$. You will get hired after the next interview if $c \ge Cp(1-p)^{k+1}$, so if $p_1$ is the solution to $c = Cp_1(1-p_1)^{k+1}$ then you will get hired after one more interview if $p_1 \le p \le p_0$. The probability of this is

What about the expected number of interviews? Assuming you are a “good” candidate from the point of view of the company, you will need to keep interviewing until you have done the number of interviews given by Equation $\eqref{eq:1}$. Since this depends on $p$, you must integrate over the possible values of $p$ to get your expected number $E$ of remaining interviews

Should I agree to one more interview?

Let’s put in some numbers. Suppose you only have the patience for one more interview. Suppose your credence about $p$ is given by a beta distribution with a mode of $0.77$. Let’s take it to be $\mathrm{Beta}(2, 1.3)$. Suppose hiring a bad candidate has the same cost to the company as $500$ interviews, so that $c=1$ and $C=500$. Then the following R code calculates the probability of getting an offer after one more interview.

pp <- seq(0, 1, 0.001)

findroot <- function(k, C, c){
  fpp <- C*pp*(1-pp)^k - c
  pmax <- pp[which.max(fpp)[1]]
  uniroot(function(p) C*p*(1-p)^k - c , c(pmax, 1))$root
}

c <- 1 # change to 10 to get negative E
C <- 500
N <- 30

# parameters for beta distribution
mode_beta <- 0.77
alpha <- 2

p <- rep(0, N + 1)
for (i in 1:length(p)) p[i] <- findroot(i, 500, 1)

f <- function(x) dbeta(x, alpha, (alpha-1)/mode_beta - (alpha-2))

pH1 <- E <- rep(0, N)
for (i in 1:N){
  # Equation (1)
  pH1[i] <- 1 - integrate(f, 0, p[i+1])$value/integrate(f, 0, p[i])$value
  
  # Equation (2)
  integrand <- function(p) (f(p)/log(1-p)) * log(c/(C*p))
  numeratorE <- integrate(integrand, 0, p[i])$value
  E[i] <- -i + numeratorE/integrate(f, 0, p[i])$value
  }

The result is shown in the blue line in the following figure.

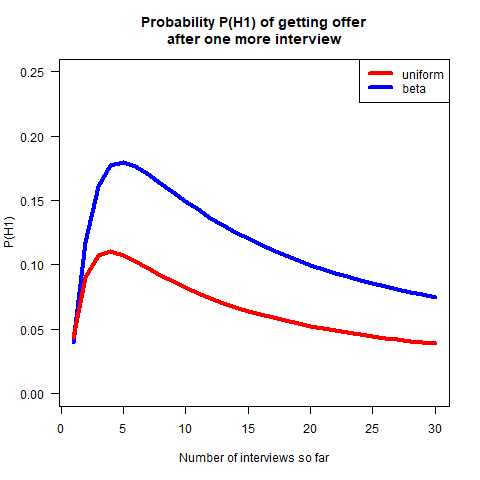
What’s surprising is that after you’ve done five interviews, your probability of getting an offer after the next interview goes down with the number of interviews you do. This is because your estimate of $p$ gets lower and lower as you are invited to more interviews. In other words, you might say that you are discovering that HR is less and less competent.

The red line in the figure shows, for comparison, what happens if your initial credence about $p$ is given by a uniform distribution. In this case, small values of $p$ are even more likely (you are even less confident about HR) and so your probability of getting hired is lower (a less competent HR will require more interviews before hiring you.)

How many more interviews am I going to need to do?

It therefore should come as no surprise that the expected number of interviews remaining goes up as the number of interviews increases, as the following figure shows. If you start with a $\mathrm{Beta}(2, 1.3)$ credence then, after $29$ interviews, you would expect to need a whopping sixteen more interviews before being hired.

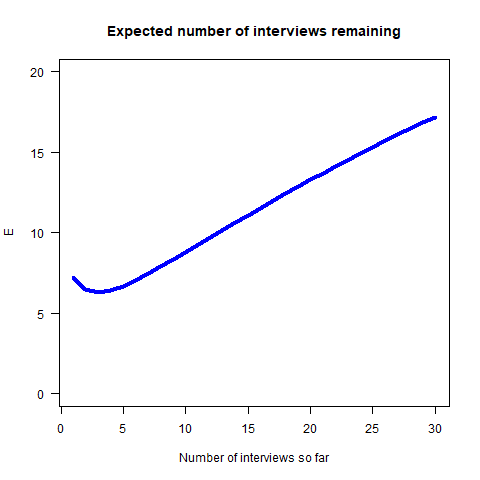
The Punchline

But why is there no red line in the second figure? What happens if you start with a uniform credence about $p$? Well, I’m glad you asked! In this case, the integral in Equation $\eqref{eq:3}$ diverges. That means that it doesn’t have a finite value. Your expected number of interviews remaining until you are hired is $E = \infty$. Although the interview process will end, on average it will be so long that, as you learn more and more about how bad the company is at doing interviews, it will effectively take forever. You are trapped in a never-ending interview hell.

Thanks for reading! And don’t have nightmares…