Thuenen's Natural Wage and the K-shaped Economy

Johann Heinrich von Thünen (1783-1850) was a German agronomist, agricultural reformer, and textbook author. If you look his name up on the internet, you’ll find that he is best remembered for his model of land use, which seems to have made its way onto the Advanced Placement Geography syllabus in the United States. However, this wasn’t always the case. In a 1955 essay, George Stigler wrote:

We like to associate each eminent economist with the doctrine he originated. Jevons—marginal utility; Walras—general equilibrium; Marshall—quasi-rents, long and short run; Wicksteed—Euler’s Theorem; Pigou—private and social marginal products; Thünen—√ap; and so it goes on.

I’ve never encountered $\sqrt{ap}$ in an economics textbook, so I decided to spend some time researching what it is all about. This was more difficult than I expected, since the formula and the argument behind it are widely believed to be flawed. Nevertheless, it turned out to be quite interesting. In particular, when I attempted to generalise von Thünen’s formula to a slightly different context, I stumbled upon a quite extraordinary numerical punchline.

This post, then, is all about what $\sqrt{ap}$ is, why Thünen thought it was important enough to be carved on his tombstone and what, if anything, it can tell us about the post-1980 world.

von Thünen

There’s a short biography of von Thünen in a 1969 paper by Dickinson. He was a wealthy landowner who ran an estate under near-mediaeval conditions, but who also cared deeply about the welfare of his employees. His book Der isolierte Staat was the fruit of long years of patiently gathering data and reasoning about economics from first principles.

An article by Blaug provides a reader’s guide to Der isolierte Staat (described as a “formless monster”). The first volume was published in 1826 and the second posthumously in 1850. There is also a third volume published in 1863. It’s the second volume which contains the famous $\sqrt{ap}$ formula for the natural wage. I worked through a few chapters of the book and found it to be surprisingly readable. It’s clear that the author wants to be understood. He often writes down a formula, then immediately gives a numerical example, then continues with further reasoning. He doesn’t omit any steps. Nevertheless, it’s not always clear what he’s getting at. Fortunately an 1895 article by H. L. Moore explains the main ideas.

The Natural Wage

In von Thünen’s isolated state, there are a large number of farms. Each farm supports one farmer who produces $p$ units of produce per year. The farm is owned by a landowner who pays the farmer a wage $w$. Everything is measured in bushels of rye. If $a$ is the amount required for subsistence, the farmer’s wage is $w = a + y$. The landowner therefore receives $p-(a+y)$.

The isolated state is assumed to have plenty of space for new farms. Von Thünen’s genius idea is to ask: what would happen if a group of farmers got fed up with working for landowners and decided to crowdfund a new farm?

To answer this, you need to make some assumptions on what it would cost to set up a new farm. Thünen spends a great deal of time discussing capital (including a lengthy digression about coconuts¹) but the upshot is that the required capital is assumed to be proportional to labour, so you may as well assume that you can set up a new farm with labour alone.

Suppose it takes one farmer to set up a new farm and that they are willing to work for subsistence wages while doing so. The crowdfunding farmers can finance this with their own wages. Each crowdfunder needs to use $a$ bushels of rye just to stay alive and in working order, but gets a surplus $w-a=y$ to spend or invest as they like. The setter-upper of the new farm also requires $a$ bushels, so the minimum number of crowdfunders required is

Once the new farm is set up, a labourer needs to be hired to work the farm. The labourer needs to be paid at least $a+y$, otherwise they might as well work for one of the existing landowners. The new farm therefore produces a surplus $p-(a+y)$ which will be shared among the $a/y$ crowdfunders plus the person who did the work of setting up the new farm, which is $1 + a/y$ people in total. Each of these people will earn

per year. If you allow $y$ to vary and maximise this quantity, you find that

and therefore $\sqrt{ap}$ is the wage level which maximises the return for each person in the group who decided to build the new farm. This is what Thünen called the natural wage.

Objections

The first problem with this is that it’s not clear what the natural wage actually means. It can’t be the wage that would hold in some sort of long-run equilibrium, because there’s nothing to stop the landowners from paying a surplus $y=0$ in the first place, and preventing the whole process from happening.

The key passage seems to be in Section 15 of the book:

Die Bestimmung des Arbeitslohns ist hier in die Hände der Arbeiter selbst gelegt, und der aus der Bestimmung der Arbeiter hervorgehende Lohn ist, wie vorhin nachgewiesen, normierend für den ganzen isolierten Staat.

Die Willkür der Arbeiter findet bei dieser Feststellung ihres Lohns keine andere Schranke als die des eigenen Interesses.

In other words, the crowdfunders are free to choose $a+y$, the wage they pay themselves but must also pay the labourer who works on their new farm, and it’s in everybody’s best interest to choose the $y$ that maximises the annual return per crowdfunder (which is also the return the extra labourer would get if they invested their own surplus $y$ in a similar crowdfunding venture).

So the natural wage is the wage that people would choose if they were playing the roles of landowners and labourers at the same time and were trying to maximise their annual return on their investment. As Dickinson says, it’s a normative result (a statement about what should be, not a prediction.)

A further objection is discussed by Blaug. It seems that this analysis neglects the time element. It’s not clear how long it would take to set up the new farm and how much interest would be foregone in the meantime. It’s also not clear that people would want to maximise the return on one year of investment. Wouldn’t they want to maximise their lifetime return instead? What if they save the extra income from the new farm and invest in a new crowdfunding project? The mathematics seems to get more complicated. But I don’t think that this argument necessarily means that $\sqrt{ap}$ is bad as a first approximation to what’s going on.

In some ways it’s understandable that an enlightened landowner like von Thünen would find this formula beguiling. It’s mathematically very neat (the natural wage is the geometric mean of the minimum possible wage and the maximum possible wage) and the natural wage turns out to be surprisingly low, which I suppose means that he could pay his workers relatively little without being troubled by his conscience.

Natural Wage with Capital

In the course of trying to understand the derivation of the natural wage, I wondered what would happen if capital was included as a separate factor of production. The isolated state has a production function $Y = pL$ which is just a Cobb-Douglas function in which capital $K$ is in fixed proportion to labour $L$, so what happens if you copy the same argument for a more general production function?

Suppose that there is a technology which takes capital $K$ and labour $L$ as inputs and produces an output of $Y = f(K, L)$. Suppose wages are not determined by the marginal product of labour, but instead workers earn a wage $w = a+y$ where $a$ is a subsistence wage and $y$ is a surplus. Suppose capital can be rented at a rate $r$. Suppose a group of workers crowdfund a new production facility by saving their surpluses $y$ to rent $K_0$ units of capital at rate $r$ and $L_0$ units of labour at rate $a$ (the subsistence wage). The total number of workers required to crowdfund and set up the new facility is

Once the new facility is set up, the owners can rent $K_1$ units of capital and $L_1$ units of labour (at rate $w = a+y$) to produce $f(K_1, L_1)$. The profit per owner is therefore

Following von Thünen we can maximise this and get

which yields

and

To make progress, note that the factor

has no global maximum in general.² However, since the workers who crowdfunded the new facility need to hire capital and labour before they can produce, it makes sense that they cannot hire more than $rK_0 + aL_0$ worth in total. Therefore, let’s assume that $K_1 = K_0$ and $L_1 = L_0$. The equation for $y$ simplifies to

Note that if $K_0 = 0$ and $f(K, L) = pL$ then this reduces to $w = \sqrt{ap}$.

Now suppose $f(K,L) = AK^\alpha L^{1-\alpha}$ is Cobb-Douglas. Suppose that the factor price of capital is equal to its marginal product. Let $Y=f(K_0, L_0)$. Then $\alpha Y = rK_0$ and

If $a$ is small and $Y/L_0$ is relatively large then the first term under the square root sign will dominate, and so

In contrast, if labour is paid its marginal product then the wage will be

which means that if workers and capital-owners are effectively the same people, it will be in their interest to pay themselves a wage which is lower than the marginal product of their labour by a factor of

If $\alpha = 1/3$, which is a standard choice of parameter in the Cobb-Douglas function because it provides a good fit to the economy of early twentieth-century America, then

Wages and Productivity

After making this calculation, I wondered how closely it fitted the facts. There’s a famous graph showing a disconnect between wages and productivity beginning in the early 1970s. One version is shown in a FRED blog post from 2023.

The graph plots an index of US real wages and an index of US productivity measured as GDP/hours worked. I used R to look at what happened to the relationship between real wages and productivity before and after the election of Ronald Reagan at the end of 1980. The FRED data is saved as fredgraph.xlsx.

library(readxl)
df <- read_excel("fredgraph.xlsx", sheet=
                   "Quarterly")
df$after_r <- (df$observation_date >= "1980-10-01 UTC")

# fit regression lines wages ~ productivity
m1 <- lm(COMPNFB_CPIAUCSL ~ OPHNFB_NBD19700101, data=df[df$after_r <= 0,])
m2 <- lm(COMPNFB_CPIAUCSL ~ OPHNFB_NBD19700101, data=df[df$after_r > 0, ])

# plot colours
cols <- rep(rgb(0, 100/255, 0, 0.2), nrow(df))
cols[df$after_r] <- rgb(1, 0, 0, 0.2)

plot(df$OPHNFB_NBD19700101, df$COMPNFB_CPIAUCSL, col=cols,
     pch=19, xlab="Productivity", ylab="Wages", las=1, cex=1.5)
abline(coef(m1), col="darkgreen", lty=2, lwd=2)
abline(coef(m2), col="red", lty=2, lwd=2)
legend("topleft", lty=2, col=c("darkgreen", "red"), lwd=2,
       legend=c("Before Reagan", "After Reagan"))

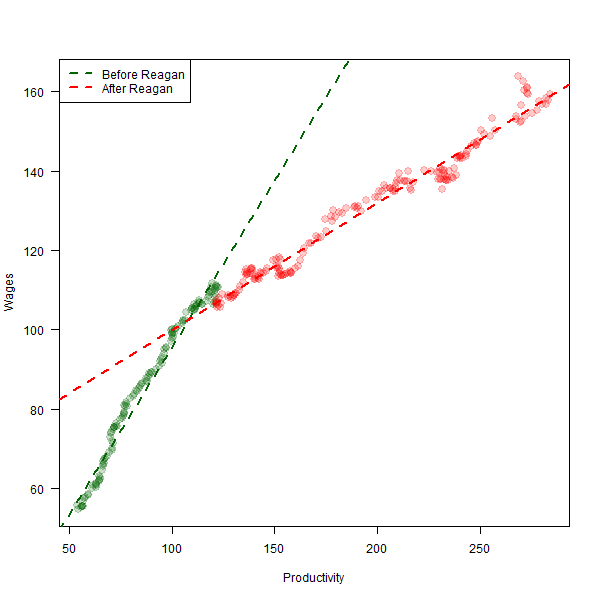
The ratio of the slope of the After Reagan line to the slope of the Before Reagan line is

coef(m2)[2]/coef(m1)[2]
# OPHNFB_NBD19700101 
#          0.3799075 

which,is remarkably close to $\frac{\sqrt{3}-1}{2} \approx 0.366$ which the modified Thünen model predicts.³

In other words, the relationship between wages and productivity after 1980 behaves almost exactly as though people have stopped getting all their income from work and started acting as if they are simultaneously workers and business owners. Why? I found one possible explanation in Debt: the first 5000 years by David Graeber. This was an extremely entertaining read full of bizarre and provocative ideas, one of which, proposed in the last chapter of the book, is the suggestion that neoliberalism is in some sense Marxist. In discussing the economics of Reagan and Thatcher, Graeber says:

All of this is not to say that the people of the world were not being offered something: just that, as I say, the terms had changed. In the new dispensation, wages would no longer rise, but workers were encouraged to buy a piece of capitalism. Rather than euthanize the rentiers, everyone could now become rentiers—effectively, could grab a chunk of the profits created by their own increasingly dramatic rates of exploitation.

In other words, deregulating markets and selling off state assets is one way of trying to put the means of production into the hands of workers.

Unfortunately, it seems that there is no way of doing this without creating massive inequality. Selling the assets would work perfectly if every potential buyer had the same level of wealth, but they don’t. Other approaches may be even worse. In the 1990s Russia tried voucher privatisation, which resulted in former state-owned industries falling into the hands of criminal gangs. And even earlier, the Russian revolutionaries used violence to seize private industries and give them to the workers themselves, but that ended in a similar result. In New Zealand our government always said that it wanted the shares of sold-off state-owned assets to go into the hands of Mums and Dads. Why Mums and Dads? Because the wealthier Mums and Dads were old. They were the ones who had accumulated enough lifetime wealth from wages to be able to buy the assets. Well, they did buy the assets. They bought all of them. Then they bought all the houses too.

In the US, people have started talking about a K-shaped economy in which the gap between rent-collecting asset owners and non-asset owning wage-earners grows at an ever-increasing pace. It’s interesting that a discredited nineteenth-century theory of feudalism fits such an economy so well.

1: Wenn wir den Ursprung des Kapitals und den Zustand der Gesellschaft, in welchem der mit keinem Kapital versehene Mensch bloß durch seine Arbeit subsistieren und selbst einiges Kapital schaffen kann, uns vergegenwärtigen wollen, so müssen wir uns in Gedanken nach den Tropenländern versetzen. It’s not clear exactly why.

2: This is because $a$ is not equal to the marginal product of labour, so the payments to factors of production do not exhaust the whole of the output.

3: Since the wage index has the form $\beta w + \gamma$ for some $\beta$ and $\gamma$ and the productivity index has the form $\beta’(Y/L) + \gamma’$ for some $\beta’$ and $\gamma’$, the predicted value for the ratio of the slopes of the two regression lines is $\frac{\sqrt{\alpha}-\alpha}{1-\alpha}$.